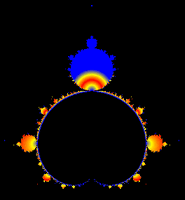
 Tanto
el conjunto de Mandelbrot (en lo que sigue conjunto M)
como los conjuntos de Julia (en lo que sigue conjuntos
J) son objetos
fractales obtenidos a partir de algoritmos muy sencillos que dan lugar, sin embargo, a una infinitud de extraordinarias
imágenes. Aunque el estudio de las iteraciones complejas
que las originan se remonta a la segunda década del siglo
XX con los trabajos de Gaston Julia y Pierre Fatou,
no fue hasta 1980 cuando Benoît
Mandelbrot obtuvo la primera imagen del conjunto que lleva
su nombre. Tanto
el conjunto de Mandelbrot (en lo que sigue conjunto M)
como los conjuntos de Julia (en lo que sigue conjuntos
J) son objetos
fractales obtenidos a partir de algoritmos muy sencillos que dan lugar, sin embargo, a una infinitud de extraordinarias
imágenes. Aunque el estudio de las iteraciones complejas
que las originan se remonta a la segunda década del siglo
XX con los trabajos de Gaston Julia y Pierre Fatou,
no fue hasta 1980 cuando Benoît
Mandelbrot obtuvo la primera imagen del conjunto que lleva
su nombre.
A continuación propongo un sencillo programa de interfaz
gráfica que se puede descargar para explorarlos. Además,
en dos apéndices, expongo por un lado el algoritmo utilizado para dibujar el conjunto M (por si alguien se anima
a programarlo), y por otro algo de teoría para los más matemáticos.
El programa MJ-1.exe
 Son dos las cosas que vamos a poder hacer con este programa:
una es viajar a través del conjunto M mediante un zoom de enorme poder de ampliación. La otra es obtener
los conjuntos J asociados a los distintos valores complejos
utilizando el conjunto M como guía. La versión
2.0 permite obtener dichos conjuntos directamente a partir del
valor del parámetro complejo c. Son dos las cosas que vamos a poder hacer con este programa:
una es viajar a través del conjunto M mediante un zoom de enorme poder de ampliación. La otra es obtener
los conjuntos J asociados a los distintos valores complejos
utilizando el conjunto M como guía. La versión
2.0 permite obtener dichos conjuntos directamente a partir del
valor del parámetro complejo c.
Para operar el programa solo es necesario conocer dos cosas: el conjunto
M es único y da lugar a una única imagen, mientras que
por cada punto de esa imagen tendremos un conjunto de Julia distinto.
Para obtener ampliaciones de cualquier imagen, con el botón
izquierdo del ratón pulsado se marca la zona que se quiere
ampliar y se suelta: la nueva imagen se generará automáticamente.
Si lo que se quiere es ver el conjunto de Julia asociado a un punto
bastará pulsar sobre el punto con el botón derecho del
ratón: una pequeña muestra del conjunto aparecerá
en la esquina inferior izquierda de la pantalla, muestra que se podrá
ampliar posteriormente si así se desea.
La riqueza de formas de los distintos conjuntos J es algo realmente
sorprendente, y más aún la complejidad del conjunto
M, pues este es una especie de diccionario gráfico de los anteriores:
en cada uno de sus puntos, si ampliamos lo suficiente la imagen a
su alrededor, obtendremos una imagen similar a la del conjunto J que
le corresponde. Dicho de otro modo: el conjunto M contiene en su interior
todas las formas que podemos encontrar en los conjuntos J.
La autosimilitud del conjunto M se pone de manifiesto en las infinitas
copias de sí mismo que contiene, copias todas ligeramente distintas,
pero todas con un inconfundible aire de familia. Otra de las sorpresas
es que es un conjunto conexo, lo que implica que lo que parecen copias
aisladas siempre están unidas al cuerpo principal mediante
finos hilillos muchas veces invisibles a causa de las limitaciones
del hardware.
Hablando de limitaciones: el conjunto de Mandelbrot y los conjuntos
de Julia tienen un infinito nivel de detalle. Si las ampliaciones
en algún momento empiezan a perder definición y se pixelizan se debe únicamente a las limitaciones del lenguaje y del procesador.
Instalación
Es sencilla: crea en tu disco una carpeta con el nombre que quieras
y descarga en ella el programa mj-1.exe.
El programa puede residir en cualquier lugar, pero la opción
de grabación almacenará los ficheros con las imágenes
seleccionadas en la carpeta donde esté el programa, por lo
que conviene que crees una carpeta independiente para él.
(Para pasar las imágenes obtenidas a un fichero en formato
jpg, gif o similares se puede utilizar un capturador
de imágenes o, simplemente, la tecla "Impr Pant"
y después pegar en algún programa gráfico).
Modos de representación
Las imágenes pueden obtenerse en cuatro estilos o modos distintos:
- Tiempo de escape: una de las maneras más frecuentes
de representar gráficamente estos conjuntos hace uso del
llamado algoritmo de tiempo de escape: consiste en medir
la velocidad con la que los términos de las sucesiones divergentes
superan en módulo cierto valor. De esta manera se consigue
algo parecido a las curvas de nivel de los mapas topográficos,
con unas imágenes increíblemente ricas en detalles.
La zona coloreada que aparece a su alrededor, aunque tiene un significado
matemático, no pertenece propiamente al conjunto.
- Convergencia: en este modo se intenta medir la velocidad
con la que los puntos convergentes tienden a su límite. Las
únicas zonas interesantes para obtener conjuntos J son los
bordes del conjunto M, aunque, eso sí, resultan muy interesantes.
- Descomposición: según el argumento de las
iteraciones se dibuja el punto de un color u otro, obteniéndose
con ello una descomposición dicotómica.
- Inversión: en este modo se fija una circunferencia
y todo lo que hay fuera de ella se lleva a su interior y lo que
habían en el interior se lleva fuera. Vamos, que le damos
la vuelta al plano como si fuese un calcetín.
Guía de viaje
En la imagen se pueden ver algunos ejemplos de conjuntos J y la zona
del conjunto M donde se pueden localizar. Son solo unas sugerencias
para iniciar el viaje (recuérdese que nos enfrentamos a infinitas
imágenes distintas).

También puede servir de orientación la
descripción de Clarke del conjunto M.
Apéndice 1: El código
La rutina que representa el conjunto M es sorprendentemente sencilla
(la de los conjuntos J es esencialmente la misma). La que aquí
transcribo está en Pascal, pero se puede traducir fácilmente
a cualquier otro lenguaje.
procedure mandelbrot;
var n,x,y: integer;
x1,y1,xx,yy,xx2, mod2:double;
tecla:char;
inch,incv,a,b,yy2: double;
valmax, iter, difh,difv: integer;
begin
valmax:=10000; {valor de comparación para controlar
la divergencia}
iter:=100; {número máximo de iteraciones}
difh:=400; {ancho de la imagen en pantalla}
difv:=400; {alto de la imagen en pantalla}
inch:=(0.8-(-2.2))/difh; {[-2.2, 0.8] intervalo horizontal a representar}
incv:=(1.5-(-1.5))/difv; {[-1.5, 1.5] intervalo vertical a representar}
for x:=1 to difh do begin {recorremos el eje horizontal}
for y:=1 to difv do begin {recorremos el eje vertical}
x1:= -2.2 + x*inch;
y1:= 1.5 - y*incv;
n:=0;
xx:=0; {inicializamos la semilla}
yy:=0;
repeat; begin {lo siguiente se repite hasta que n>iter o
mod2>valmax}
n:= n + 1;
xx2 := xx*xx-yy*yy; {cuadrado del complejo xx + yyi}
yy := 2*xx*yy;
xx:=xx2;
xx := xx+x1; {se suma el complejo x1+y1i}
yy := yy+y1;
mod2:= xx*xx+yy*yy; {calculo del cuadrado del modulo}
end; until (n>iter) or (mod2>valmax);
if n<iter+1 then putpixel(x,y,n); {se pinta el punto (x,
y) con el color n}
end;
end;
end;
Apéndice 2: Teoría
Conjuntos de Julia (léase Juliá)
Técnicamente, cada uno de estos conjuntos es la frontera del
conjunto de los puntos del plano
complejo que divergen bajo la iteración zn+1 = zn2 + c, donde c es un número complejo fijo. Esta fórmula
define una sucesión por recurrencia de la siguiente manera:
se coge un valor complejo, al que llamamos z1, se
eleva al cuadrado y se le suma c. El resultado obtenido es z2, que se convierte en el valor de partida para
calcular, repitiendo el proceso, z3 , y así
sucesivamente:
z2 = z12 + c
z3 = z22 + c
z4 = z32 + c
...
La secuencia z1, z2, z3,...
es una sucesión que dependiendo del z1 elegido
podrá diverger o no, es decir, tender a infinito cuando el número
de iteraciones tienda a infinito o no.
Si el proceso anterior se realiza para cada uno de los z1 de una región del plano complejo estaremos clasificando dichos
puntos en dos clases, la de aquellos que divergen y la de los que
no. Pues bien, el conjunto de Julia será la frontera del conjunto
de los puntos que generan sucesiones divergentes.
En el proceso anterior hemos mantenido fijo el valor del número
compljo c, lo cual implica que hay un conjunto de Julia para
cada valor de c, es decir, infinitos, aunque se pueden reconocer
un cierto número de familias de imágenes similares.
Conjunto de Mandelbrot
Los conjuntos de Julia pueden ser de dos tipos: conexos (de una sola
pieza, para entendernos), o completamente desconectados (cada punto
es como una partícula de polvo separada de las demás).
Pues bien, el conjunto de Mandelbrot se define como el conjunto de
los valores complejos de c para los que el correspondiente
conjunto de Julia es conexo. Así dicho podría parecer
difícil representar tal conjunto, pero resulta que no lo es,
gracias a un resultado del propio Julia, que dice lo siguiente: el
conjunto de Julia asociado al complejo c es conexo si la sucesión
obtenida por la iteración zn+1 = zn2 + c para z1 = 0 no diverge.
Uno de los resultados más sorprendentes acerca del conjunto
de Mandelbrot es que es un conjunto conexo, es decir, de una sola
pieza, como demostraron A. Douady y J.H.
Hubbard.
|
 Tanto
el conjunto de Mandelbrot (en lo que sigue conjunto M)
como los conjuntos de Julia (en lo que sigue conjuntos
J) son objetos
fractales obtenidos a partir de algoritmos muy sencillos que dan lugar, sin embargo, a una infinitud de extraordinarias
imágenes. Aunque el estudio de las iteraciones complejas
que las originan se remonta a la segunda década del siglo
XX con los trabajos de Gaston Julia y Pierre Fatou,
no fue hasta 1980 cuando Benoît
Mandelbrot obtuvo la primera imagen del conjunto que lleva
su nombre.
Tanto
el conjunto de Mandelbrot (en lo que sigue conjunto M)
como los conjuntos de Julia (en lo que sigue conjuntos
J) son objetos
fractales obtenidos a partir de algoritmos muy sencillos que dan lugar, sin embargo, a una infinitud de extraordinarias
imágenes. Aunque el estudio de las iteraciones complejas
que las originan se remonta a la segunda década del siglo
XX con los trabajos de Gaston Julia y Pierre Fatou,
no fue hasta 1980 cuando Benoît
Mandelbrot obtuvo la primera imagen del conjunto que lleva
su nombre.